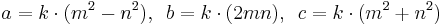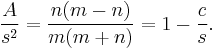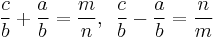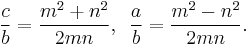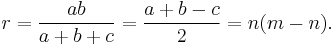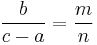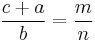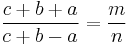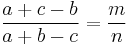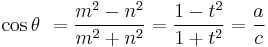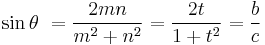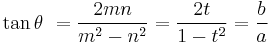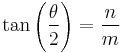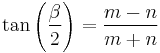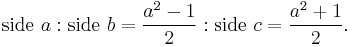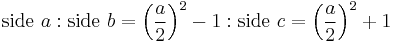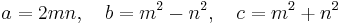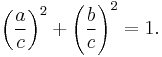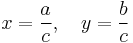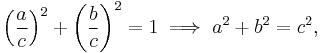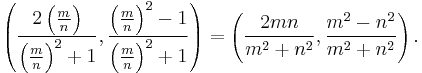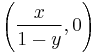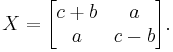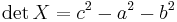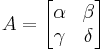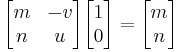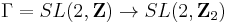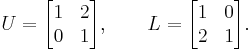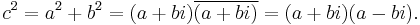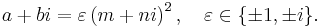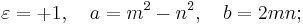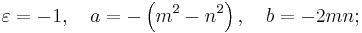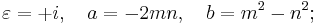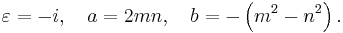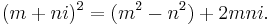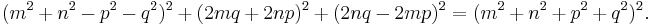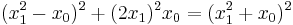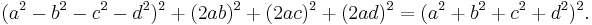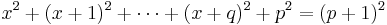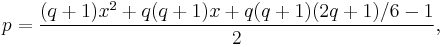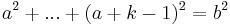Pythagorean triple

A Pythagorean triple consists of three positive integers a, b, and c, such that a² + b² = c². Such a triple is commonly written (a, b, c), and a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A primitive Pythagorean triple (PPT) is one in which a, b and c are pairwise coprime. A right triangle whose sides form a Pythagorean triple is called a Pythagorean triangle.

The name is derived from the Pythagorean theorem, stating that every right triangle has side lengths satisfying the formula a² + b² = c²; thus, Pythagorean triples describe the three integer side lengths of a right triangle. However, right triangles with non-integer sides do not form Pythagorean triples. For instance, the triangle with sides a = b = 1 and c = √2 is right, but (1, 1, √2) is not a Pythagorean triple because √2 is not an integer. Moreover, 1 and √2 do not have an integer common multiple because √2 is irrational.

Examples

There are 16 primitive Pythagorean triples with c ≤ 100:

( 3 , 4 , 5 )	( 5, 12, 13)	( 7, 24, 25)	( 8, 15, 17)
( 9, 40, 41)	(11, 60, 61)	(12, 35, 37)	(13, 84, 85)
(16, 63, 65)	(20, 21, 29)	(28, 45, 53)	(33, 56, 65)
(36, 77, 85)	(39, 80, 89)	(48, 55, 73)	(65, 72, 97)

Each one of these low-c points forms one of the more easily-recognizable radiating lines in the scatter plot.

Additionally these are all the primitive Pythagorean triples with 100 < c ≤ 300:

(20, 99, 101)	(60, 91, 109)	(15, 112, 113)	(44, 117, 125)
(88, 105, 137)	(17, 144, 145)	(24, 143, 145)	(51, 140, 149)
(85, 132, 157)	(119, 120, 169)	(52, 165, 173)	(19, 180, 181)
(57, 176, 185)	(104, 153, 185)	(95, 168, 193)	(28, 195, 197)
(84, 187, 205)	(133, 156, 205)	(21, 220, 221)	(140, 171, 221)
(60, 221, 229)	(105, 208, 233)	(120, 209, 241)	(32, 255, 257)
(23, 264, 265)	(96, 247, 265)	(69, 260, 269)	(115, 252, 277)
(160, 231, 281)	(161, 240, 289)	(68, 285, 293)

Generating a triple

Main article: Formulas for generating Pythagorean triples

Euclid's formula^[1] is a fundamental formula for generating Pythagorean triples given an arbitrary pair of positive integers m and n with m > n. The formula states that the integers

$a = m^2 - n^2 ,\ \, b = 2mn ,\ \, c = m^2 %2B n^2$

form a Pythagorean triple. The triple generated by Euclid's formula is primitive if and only if m and n are coprime and m–n is odd. If both m and n are odd, then a, b, and c will be even, and so the triple will not be primitive; however, dividing a, b, and c by 2 will yield a primitive triple if m and n are coprime.^[2]

Every primitive triple (possibly after exchanging a and b) arises from a unique pair of coprime numbers m, n, one of which is even. It follows that there are infinitely many primitive Pythagorean triples. This relationship of a and b to m and n from Euclid's formula is referenced throughout the rest of this article.

Despite generating all primitive triples, Euclid's formula does not produce all triples. This can be remedied by inserting an additional parameter k to the formula. The following will generate all Pythagorean triples (although not uniquely):

$a = k\cdot(m^2 - n^2) ,\ \, b = k\cdot(2mn) ,\ \, c = k\cdot(m^2 %2B n^2)$

where m, n, and k are positive integers with m > n.

That these formulas generate Pythagorean triples can be verified by expanding a² + b² using elementary algebra and verifying that the result coincides with c² (although this does not prove that it generates all such triples). Many other formulas for generating triples have been developed since the time of Euclid.

Each primitive Pythagorean triangle has a ratio of area to squared semiperimeter that is unique to itself and is given by^[3]

$\frac{A}{s^2} = \frac{n(m-n)}{m(m%2Bn)} = 1-\frac{c}{s}.$

Proof of Euclid's formula

That satisfaction of Euclid's formula by a, b, c is sufficient for the triangle to be Pythagorean is apparent from the fact that for integers m and n, the a, b, and c given by the formula are all integers, and from the fact that 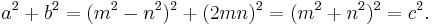$a^2%2Bb^2 = (m^2 - n^2)^2 %2B (2mn)^2 = (m^2 %2B n^2)^2 = c^2.$

A simple proof of the necessity that a, b, c be expressed by Euclid's formula for any primitive Pythagorean triple is as follows.^[4] All such triples can be written as (a, b, c) where a²+b²=c² and a, b, c are pairwise coprime, and where b and c have opposite parities. (If c had the same parity as both legs, then if all were even the parameters would not be coprime, and if all were odd then a²+b²=c² would equate an even to an odd.) From 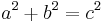$a^2%2Bb^2=c^2$ we obtain 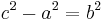$c^2-a^2=b^2$ and hence 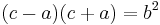$(c-a)(c%2Ba)=b^2$ . Then 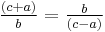$\tfrac{(c%2Ba)}{b}=\tfrac{b}{(c-a)}$ . Since 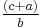$\tfrac{(c%2Ba)}{b}$ is rational, we set it equal to 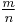$\tfrac{m}{n}$ in lowest terms; and we observe that 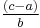$\tfrac{(c-a)}{b}$ equals the reciprocal of 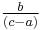$\tfrac{b}{(c-a)}$ and hence equals the reciprocal of 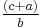$\tfrac{(c%2Ba)}{b}$ , and thus equals 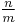$\tfrac{n}{m}$ . Then solving

$\frac{c}{b}%2B\frac{a}{b}=\frac{m}{n}, \ \, \frac{c}{b}-\frac{a}{b}=\frac{n}{m}$

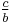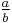for $\tfrac{c}{b}$ and $\tfrac{a}{b}$ gives

$\frac{c}{b}=\frac{m^2%2Bn^2}{2mn}, \ \,\frac{a}{b}=\frac{m^2-n^2}{2mn}.$

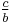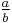Since $\tfrac{c}{b}$ and $\tfrac{a}{b}$ are fully reduced by assumption, the numerators can be equated and the denominators can be equated if and only if the right side of each equation is fully reduced; given the previous specification that 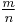$\tfrac{m}{n}$ is fully reduced, implying that m and n are coprime, the right sides are fully reduced if and only if m and n have opposite parity (one is even and one is odd) so that the numerators are not divisible by 2. (And m and n must have opposite parity: if both were odd then dividing through 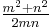$\tfrac{m^2%2Bn^2}{2mn}$ by 2 would give the ratio of two odd numbers; equating this ratio to 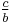$\tfrac{c}{b}$ , which is a ratio of two numbers with opposite parities, would give conflicting parities when the equation is cross-multiplied.) So equating numerators and equating denominators, we have Euclid's formula 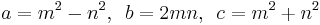$a = m^2 - n^2 ,\ \, b = 2mn ,\ \, c = m^2 %2B n^2$ with m and n coprime and of opposite parities.

A longer but more commonplace proof is given in Maor (2007)^[5] and Sierpinski (2003).^[6]

Interpretation of parameters in Euclid's formula

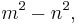
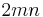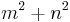Suppose the sides of a Pythagorean triangle are $m^2-n^2,$ $2mn$ , and $m^2%2Bn^2$ , and suppose the angle between the leg 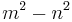$m^2-n^2$ and the hypotenuse 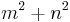$m^2%2Bn^2$ is denoted as 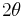$2\theta$ . Then a right triangle with legs $m$ and $n$ has the angle $\theta$ between the leg $m$ and the (not necessarily rational) hypotenuse.^[7]

Elementary properties of primitive Pythagorean triples

The properties of a primitive Pythagorean triple (PPT) (a,b,c) with a < b < c (without specifying which of a or b is even and which is odd) include:

(c − a)(c − b)/2 is always a perfect square. This is particularly useful in checking if a given triple of numbers is a Pythagorean triple, but it is only a necessary condition, not a sufficient one. The triple {6, 12, 18} passes the test that (c − a)(c − b)/2 is a perfect square, but it is not a Pythagorean triple. When a triple of numbers a, b and c forms a primitive Pythagorean triple, then (c minus the even leg) and one-half of (c minus the odd leg) are both perfect squares; however this is not a sufficient condition, as the triple {1, 8, 9} is a counterexample since 1² + 8² ≠ 9².
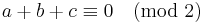
The sum of a,b,c is always an even number. In other words, $a%2Bb%2Bc \equiv 0 \pmod 2\,$
At most one of a, b, c is a square. (See Infinite descent#Non-solvability of r2 + s4 = t4 for a proof.)
There exist infinitely many primitive Pythagorean triples whose hypotenuses are squares of natural numbers.
There exist infinitely many primitive Pythagorean triples in which one of the legs is the square of a natural number.
The sum of the hypotenuse and the even leg of a primitive Pythagorean triple is the square of an odd number, and the arithmetic mean of the hypotenuse and the odd leg is a perfect square.
The area (A = ab/2) is an even congruent number.
The area of a Pythagorean triangle cannot be the square^[8]^{:p. 17} or twice the square^[8]^{:p. 21} of a natural number.
Exactly one of a, b is odd; c is odd.
Exactly one of a, b is divisible by 3.^[9]
Exactly one of a, b is divisible by 4.^[9]
Exactly one of a, b, c is divisible by 5.^[9]
Exactly one of a, b, (a + b), (b − a) is divisible by 7.
Exactly one of (a + c), (b + c), (c − a), (c − b) is divisible by 8.
Exactly one of (a + c), (b + c), (c − a), (c − b) is divisible by 9.
Exactly one of a, b, (2a + b), |2a − b|, (2b + a), (2b − a) is divisible by 11.
Exactly one of a, b, c, (2c + a), (2c + b), (2c - a), (2c - b) is divisible by 13.
All prime factors of c are primes of the form 4n + 1.
Every integer greater than 2 that is not congruent to 2 mod 4 (in other words, every integer greater than 2 which is not of the form 4n + 2) is part of a primitive Pythagorean triple.
Every integer greater than 2 is part of a primitive or non-primitive Pythagorean triple, for example, the integers 6, 10, 14, and 18 are not part of primitive triples, but are part of the non-primitive triples 6, 8, 10; 14, 48, 50 and 18, 80, 82.
There exist infinitely many Pythagorean triples in which the hypotenuse and the longer of the two legs differ by exactly one (such triples are necessarily primitive). Generalization: For every odd integer j, there exist infinitely many primitive Pythagorean triples in which the hypotenuse and the even leg differ by j².
There exist infinitely many primitive Pythagorean triples in which the hypotenuse and the longer of the two legs differ by exactly two. Generalization: For every integer k > 0, there exist infinitely many primitive Pythagorean triples in which the hypotenuse and the odd leg differ by $2k^2$ .
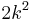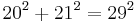There exist infinitely many Pythagorean triples in which the two legs differ by exactly one—e.g., $20^2 %2B 21^2 = 29^2$ .
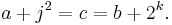
If j and k are odd positive integers, not necessarily unequal, there is exactly one primitive Pythagorean triple with $a %2B j^2 = c = b %2B 2^k.$
The hypotenuse of every primitive Pythagorean triangle exceeds the even leg by the square of an odd integer j, and exceeds the odd leg by twice the square of an integer k > 0, from which it follows that:

There are no primitive Pythagorean triples in which the hypotenuse and a leg differ by a prime number greater than 2.

For each natural number n, there exist n Pythagorean triples with different hypotenuses and the same area.
For each natural number n, there exist at least n different Pythagorean triples with the same leg a, where a is some natural number
For each natural number n, there exist at least n different Pythagorean triples with the same hypotenuse.
In every primitive Pythagorean triple, the radius of the incircle and the radii of the three excircles are natural numbers. Specifically, the radius of the incircle is 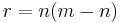$r = n(m - n)$ , and the radii of the excircles opposite the sides m²–n², 2mn, and the hypotenuse m²+n² are respectively m(m − n), n(m + n), and m(m + n).
When the area of a Pythagorean triangle is multiplied by the curvatures of its incircle and 3 excircles, the result is four positive integers 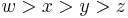$w>x>y>z$ . Integers 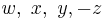$w,\text{ }x,\text{ }y,-z$ satisfy Descartes’s Circle Equation. ^[10]
There are no Pythagorean triples in which the hypotenuse and one leg are the legs of another Pythagorean triple.^[8]^{:p. 14}
The set of all primitive Pythagorean triples forms a rooted ternary tree in a natural way; see Tree of primitive Pythagorean triples.

Some relationships

The radius, r, of the inscribed circle can be found by:

$r = \frac{ab}{a%2Bb%2Bc} = \frac{a%2Bb-c}{2} = n(m-n).\$

The unknown sides of a triple can be calculated directly from the radius of the incircle, r, and the value of a single known side, b.

k = b − 2r

a = 2r + (2 r²/k)

c = a+ k = 2r + (2r² /k) + k

The solution to the 'Incircle' problem shows that, for any circle whose radius is a whole number r, setting k = 1, we are guaranteed at least one right angled triangle containing this circle as its inscribed circle where the lengths of the sides of the triangle are a primitive Pythagorean triple:

a=2r + 2r²

b=2r + 1

c=2r + 2r² + 1

The perimeter P and area L of the right triangle corresponding to a primitive Pythagorean triple triangle are

P = a + b + c = 2m(m + n)

L = ab/2 = mn(m² − n²)

Additional relationships:^[11]

$\frac{b}{c-a}= \frac{m}{n}\,$

$\frac{c%2Ba}{b}= \frac{m}{n}\,$

$\frac{c%2Bb%2Ba}{c%2Bb-a}= \frac{m}{n}\,$

$\frac{a%2Bc-b}{a%2Bb-c}= \frac{m}{n}\,$

$\cos\theta\ = {m^2-n^2 \over m^2%2Bn^2} = {1-t^2 \over 1%2Bt^2} = {a \over c}$

$\sin\theta\ = {2mn \over m^2%2Bn^2} = {2t \over 1%2Bt^2} = {b \over c}$

$\tan\theta\ = {2mn \over m^2-n^2} = {2t \over 1-t^2} = {b \over a}$

$\tan\left({\theta \over 2}\right) = {n \over m}$

$\tan\left({\beta \over 2}\right) = {m-n \over m%2Bn}$

If two numbers of a triple are known, the third can be found using the Pythagorean theorem.

A special case: the Platonic sequence

The case n = 1 of the more general construction of Pythagorean triples has been known for a long time. Proclus, in his commentary to the 47th Proposition of the first book of Euclid's Elements, describes it as follows:

Certain methods for the discovery of triangles of this kind are handed down, one which they refer to Plato, and another to Pythagoras. (The latter) starts from odd numbers. For it makes the odd number the smaller of the sides about the right angle; then it takes the square of it, subtracts unity and makes half the difference the greater of the sides about the right angle; lastly it adds unity to this and so forms the remaining side, the hypotenuse.
...For the method of Plato argues from even numbers. It takes the given even number and makes it one of the sides about the right angle; then, bisecting this number and squaring the half, it adds unity to the square to form the hypotenuse, and subtracts unity from the square to form the other side about the right angle. ... Thus it has formed the same triangle that which was obtained by the other method.

In equation form, this becomes:

a is odd (Pythagoras, c. 540 BC):

$\text{side }a�: \text{side }b = {a^2 - 1 \over 2}�: \text{side }c = {a^2 %2B 1 \over 2}.$

a is even (Plato, c. 380 BC):

$\text{side }a�: \text{side }b = \left({a \over 2}\right)^2 - 1�: \text{side }c = \left({a \over 2}\right)^2 %2B 1$

It can be shown that all Pythagorean triples are derivatives of the basic Platonic sequence (x, y, z) = p, (p² − 1)/2 and (p² + 1)/2 by allowing p to take non-integer rational values. If p is replaced with the rational fraction m/n in the sequence, the 'standard' triple generator 2mn, m² − n² and m² + n² results. It follows that every triple has a corresponding rational p value which can be used to generate a similar (i.e. equiangular) triangle with rational sides in the same proportion as the original. For example, the Platonic equivalent of (6, 8, 10) is (3/2; 2, 5/2). The Platonic sequence itself can be derived by following the steps for 'splitting the square' described in Diophantus II.VIII.

Geometry of Euclid's formula

Euclid's formulae for a Pythagorean triple

$a = 2mn,\quad b=m^2-n^2,\quad c=m^2%2Bn^2$

can be understood in terms of the geometry of rational number points on the unit circle (Trautman 1998). To motivate this, consider a right triangle with legs a and b, and hypotenuse c, where a, b, and c are positive integers. By the Pythagorean theorem, a² + b² = c² or, dividing both sides by c²,

$\left(\frac{a}{c}\right)^2 %2B \left(\frac{b}{c}\right)^2=1.$

Geometrically, the point in the Cartesian plane with coordinates

$x=\frac{a}{c},\quad y=\frac{b}{c}$

is on the unit circle x² + y² = 1. In this equation, the coordinates x and y are given by rational numbers. Conversely, any point on the unit circle whose coordinates x, y are rational numbers gives rise to a primitive Pythagorean triple. Indeed, write x and y as fractions in lowest terms:

$x=\frac{a}{c},\quad y=\frac{b}{c}$

where the greatest common divisor of a, b, and c is 1. Then, since x and y are on the unit circle,

$\left(\frac{a}{c}\right)^2 %2B \left(\frac{b}{c}\right)^2=1\implies a^2%2Bb^2=c^2,$

as claimed.

There is therefore a correspondence between points on the unit circle with rational coordinates and primitive Pythagorean triples. At this point, Euclid's formulae can be derived either by methods of trigonometry or equivalently by using the stereographic projection.

For this, suppose that P′ is a point on the x-axis with rational coordinates P′(m/n,0). Then, it can be shown by basic algebra that the point P has coordinates

$\left( \frac{2\left(\frac{m}{n}\right)}{\left(\frac{m}{n}\right)^2%2B1}, \frac{\left(\frac{m}{n}\right)^2-1}{\left(\frac{m}{n}\right)^2%2B1} \right) = \left( \frac{2mn}{m^2%2Bn^2}, \frac{m^2-n^2}{m^2%2Bn^2} \right).$

This establishes that each rational point of the x-axis goes over to a rational point of the unit circle. The converse, that every rational point of the unit circle comes from such a point of the x-axis, follows by applying the inverse stereographic projection. Suppose that P(x, y) is a point of the unit circle with x and y rational numbers. Then the point P′ obtained by stereographic projection onto the x-axis has coordinates

$\left(\frac{x}{1-y},0\right)$

which is rational.

In terms of algebraic geometry, the algebraic variety of rational points on the unit circle is birational to the affine line over the rational numbers. The unit circle is thus called a rational curve, and it is this fact which enables an explicit parameterization of the (rational number) points on it by means of rational functions.

Spinors and the modular group

Pythagorean triples can likewise be encoded into a matrix of the form

$X = \begin{bmatrix} c%2Bb & a\\ a & c-b \end{bmatrix}.$

A matrix of this form is symmetric. Furthermore, the determinant of X is

$\det X = c^2 - a^2 - b^2\,$

which is zero precisely when (a,b,c) is a Pythagorean triple. If X corresponds to a Pythagorean triple, then as a matrix it must have rank 1. Since X is symmetric, it follows from a result in linear algebra that there is a vector ξ = [m n]^T such that the outer product

$X = 2\begin{bmatrix}m\\n\end{bmatrix}[m\ n] = 2\xi\xi^T\,$

(1)

holds, where the T denotes the matrix transpose. The vector ξ is called a spinor (for the Lorentz group SO(1, 2)). In abstract terms, the Euclid formula means that each primitive Pythagorean triple can be written as the outer product with itself of a spinor with integer entries, as in (1).

The modular group Γ is the set of 2×2 matrices with integer entries

$A = \begin{bmatrix}\alpha&\beta\\ \gamma&\delta\end{bmatrix}$

with determinant equal to one: αδ − βγ = 1. This set forms a group, since the inverse of a matrix in Γ is again in Γ, as is the product of two matrices in Γ. The modular group acts on the collection of all integer spinors. Furthermore, the group is transitive on the collection of integer spinors with relatively prime entries. For if [m n]^T has relatively prime entries, then

$\begin{bmatrix}m&-v\\n&u\end{bmatrix}\begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}m\\n\end{bmatrix}$

where u and v are selected (by the Euclidean algorithm) so that mu + nv = 1.

By acting on the spinor ξ in (1), the action of Γ goes over to an action on Pythagorean triples, provided one allows for triples with possibly negative components. Thus if A is a matrix in Γ, then

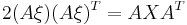
$2(A\xi)(A\xi)^T = A X A^T\,$

(2)

gives rise to an action on the matrix X in (1). This does not give a well-defined action on primitive triples, since it may take a primitive triple to an imprimitive one. It is convenient at this point (per Trautman 1998) to call a triple (a,b,c) standard if c > 0 and either (a,b,c) are relatively prime or (a/2,b/2,c/2) are relatively prime with a/2 odd. If the spinor [m n]^T has relatively prime entries, then the associated triple (a,b,c) determined by (1) is a standard triple. It follows that the action of the modular group is transitive on the set of standard triples.

Alternatively, restrict attention to those values of m and n for which m is odd and n is even. Let the subgroup Γ(2) of Γ be the kernel of the group homomorphism

$\Gamma=SL(2,\mathbf{Z})\to SL(2,\mathbf{Z}_2)$

where SL(2,Z₂) is the special linear group over the finite field Z₂ of integers modulo 2. Then Γ(2) is the group of unimodular transformations which preserve the parity of each entry. Thus if the first entry of ξ is odd and the second entry is even, then the same is true of Aξ for all A ∈ Γ(2). In fact, under the action (2), the group Γ(2) acts transitively on the collection of primitive Pythagorean triples (Alperin 2005).

The group Γ(2) is the free group whose generators are the matrices

$U=\begin{bmatrix}1&2\\0&1\end{bmatrix},\qquad L=\begin{bmatrix}1&0\\2&1\end{bmatrix}.$

Consequently, every primitive Pythagorean triple can be obtained in a unique way as a product of copies of the matrices U and L.

Parent/child relationships

Main article: Tree of Pythagorean triples

By a result of Berggren (1934), all primitive Pythagorean triples can be generated from the (3, 4, 5) triangle by using the three linear transformations T1, T2, T3 below, where a, b, c are sides of a triple:

	new side a	new side b	new side c
T1:	a − 2b + 2c	2a − b + 2c	2a − 2b + 3c
T2:	a + 2b + 2c	2a + b + 2c	2a + 2b + 3c
T3:	−a + 2b + 2c	−2a + b + 2c	−2a + 2b + 3c

If one begins with 3, 4, 5 then all other primitive triples will eventually be produced. In other words, every primitive triple will be a “parent” to 3 additional primitive triples. Starting from the initial node with a = 3, b = 4, and c = 5, the next generation of triples is

new side a	new side b	new side c
3 − (2×4) + (2×5) = 5	(2×3) − 4 + (2×5) = 12	(2×3) − (2×4) + (3×5) = 13
3 + (2×4) + (2×5) = 21	(2×3) + 4 + (2×5) = 20	(2×3) + (2×4) + (3×5) = 29
−3 + (2×4) + (2×5) = 15	−(2×3) + 4 + (2×5) = 8	−(2×3) + (2×4) + (3×5) = 17

The linear transformations T1, T2, and T3 have a geometric interpretation in the language of quadratic forms. They are closely related to (but are not equal to) reflections generating the orthogonal group of x² + y² − z² over the integers. A different set of three linear transformations is discussed in Pythagorean triples by use of matrices and_linear transformations. For further discussion of parent-child relationships in triples, see: Pythagorean triple (Wolfram) and (Alperin 2005).

Relation to Gaussian integers

Alternatively, Euclid's formulae can be analyzed and proven using the Gaussian integers.^[12] Gaussian integers are complex numbers of the form α = u + vi, where u and v are ordinary integers and i is the square root of negative one, and the units of Gaussian integers are ±1 and ±i. The ordinary integers are called the rational integer and denoted as Z. The Gaussian integers are denoted as Z[i].. The right-hand side of the Pythagorean theorem may be factored in Gaussian integers:

$c^2 = a^2%2Bb^2 = (a%2Bbi)\overline{(a%2Bbi)} = (a%2Bbi)(a-bi).$

A primitive Pythagorean triple is one in which a and b are coprime, i.e., they share no prime factors in the integers. For such a triple, either a or b is even, and the other is odd; from this, it follows that c is also odd.

The two factors z := a + bi and z* := a − bi of a primitive Pythagorean triple each equal the square of a Gaussian integer. This can be proved using the property that every Gaussian integer can be factored uniquely into Gaussian primes up to units.^[13] (This unique factorization follows from the fact that, roughly speaking, a version of the Euclidean algorithm can be defined on them.) The proof has three steps. First, if a and b share no prime factors in the integers, then they also share no prime factors in the Gaussian integers. (Assume a = gu and b = gv with Gaussian integers g, u and v and g not a unit. Then u and v lie on the same line through the origin. All Gaussian integers on such a line are integer multiples of some Gaussian integer h. But then the integer gh ≠ ±1 divides both a and b.) Second, it follows that z and z* likewise share no prime factors in the Gaussian integers. For if they did, then their common divisor δ would also divide z + z* = 2a and z − z* = 2ib. Since a and b are coprime, that implies that δ divides 2 = (1 + i)(1 − i) = i(1 − i)². From the formula c² = zz*, that in turn would imply that c is even, contrary to the hypothesis of a primitive Pythagorean triple. Third, since c² is a square, every Gaussian prime in its factorization is doubled, i.e., appears an even number of times. Since z and z* share no prime factors, this doubling is also true for them. Hence, z and z* are squares.

Thus, the first factor can be written

$a%2Bbi = \varepsilon\left(m %2B ni \right)^2, \quad \varepsilon\in\{\pm 1, \pm i\}.$

The real and imaginary parts of this equation give the two formulas

$\varepsilon = %2B1,\quad a = m^2 - n^2,\quad b = 2mn;$

$\varepsilon = -1,\quad a = -\left( m^2 - n^2 \right),\quad b = -2mn;$

$\varepsilon = %2Bi,\quad a = -2mn,\quad b = m^2 - n^2;$

$\varepsilon = -i,\quad a = 2mn,\quad b = -\left( m^2 - n^2 \right).$

For any primitive Pythagorean triple, there must be integers m and n such that these two equations are satisfied. Hence, every Pythagorean triple can be generated from some choice of these integers.

As perfect Square Gaussian integers

If we consider the square of a Gaussian integer we get the following direct interpretation of Euclid's formulae as representing a perfect square Gaussian integers.

$(m%2Bni)^2 = (m^2-n^2)%2B2mni.$

Using the facts that the Gaussian integers are a Euclidean domain and that for a Gaussian integer p 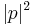$|p|^2$ is always a square it is possible to show that a Pythagorean triples correspond to the square of a prime Gaussian integer if the hypotenuse is prime.

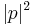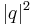If the Gaussian integer is not prime then it is the product of two Gaussian integers p and q with $|p|^2$ and $|q|^2$ integers. Since magnitudes multiply in the Gaussian integers, the product must be 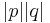$|p||q|$ , which when squared to find a Pythagorean triple must be composite. The contrapositive completes the proof.

Distribution of triples

There are a number of results on the distribution of Pythagorean triples. In the scatter plot, a number of obvious patterns are already apparent. Whenever the legs (a,b) of a primitive triple appear in the plot, all integer multiples of (a,b) must also appear in the plot, and this property produces the appearance of lines radiating from the origin in the diagram.

Within the scatter, there are sets of parabolic patterns with a high density of points and all their foci at the origin, opening up in all four directions. Different parabolas intersect at the axes and appear to reflect off the axis with an incidence angle of 45 degrees, with a third parabola entering in a perpendicular fashion. Within this quadrant, each arc centered around the origin shows that section of the parabola that lies between its tip and its intersection with its semi-latus rectum.

These patterns can be explained as follows. If 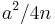$a^2/4n$ is an integer, then (a, 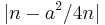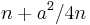$|n-a^2/4n|$ , $n%2Ba^2/4n$ ) is a Pythagorean triple. (In fact every Pythagorean triple (a, b, c) can be written in this way with integer n, possibly after exchanging a and b, since 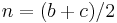$n=(b%2Bc)/2$ and a and b cannot both be odd.) The Pythagorean triples thus lie on curves given by 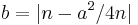$b = |n-a^2/4n|$ , that is, parabolas reflected at the a-axis, and the corresponding curves with a and b interchanged. If a is varied for a given n (i.e. on a given parabola), integer values of b occur relatively frequently if n is a square or a small multiple of a square. If several such values happen to lie close together, the corresponding parabolas approximately coincide, and the triples cluster in a narrow parabolic strip. For instance, 38² = 1444, 2 × 27² = 1458, 3 × 22² = 1452, 5 × 17² = 1445 and 10 × 12² = 1440; the corresponding parabolic strip around n ≈ 1450 is clearly visible in the scatter plot.

The angular properties described above follow immediately from the functional form of the parabolas. The parabolas are reflected at the a-axis at a = 2n, and the derivative of b with respect to a at this point is –1; hence the incidence angle is 45°. Since the clusters, like all triples, are repeated at integer multiples, the value 2n also corresponds to a cluster. The corresponding parabola intersects the b-axis at right angles at b = 2n, and hence its reflection upon interchange of a and b intersects the a-axis at right angles at a = 2n, precisely where the parabola for n is reflected at the a-axis. (The same is of course true for a and b interchanged.)

Albert Fässler and others provide insights into the significance of these parabolas in the context of conformal mappings.^[14]^[15]

Generalizations

There are several ways to generalize the concept of Pythagorean triples.

Pythagorean quadruple

Main article: Pythagorean quadruple

A set of four positive integers a, b, c and d such that a² + b²+ c² = d² is called a Pythagorean quadruple. The simplest example is (1, 2, 2, 3), since 1² + 2² + 2² = 3². The next simplest (primitive) example is (2, 3, 6, 7), since 2² + 3² + 6² = 7².

All quadruples are given by the formula

$(m^2%2Bn^2-p^2-q^2)^2%2B(2mq%2B2np)^2%2B(2nq-2mp)^2=(m^2%2Bn^2%2Bp^2%2Bq^2)^2.$

Pythagorean n-tuple

Using the simple algebraic identity,

$(x_1^2-x_0)^2 %2B (2x_1)^{2}x_0 = (x_1^2%2Bx_0)^2$

for arbitrary x₀, x₁, it is easy to prove that the square of the sum of n squares is itself the sum of n squares by letting x₀ = x₂² + x₃² + ... + x_n² and then distributing terms.^[16] One can see how Pythagorean triples and quadruples are just the particular cases x₀ = x₂² and x₀ = x₂² + x₃², respectively, and so on for other n, with quintuples given by

$(a^2-b^2-c^2-d^2)^2 %2B (2ab)^2 %2B (2ac)^2 %2B (2ad)^2 = (a^2%2Bb^2%2Bc^2%2Bd^2)^2.$

In addition, Pythagorean n-tuples (n≥3) with the first n − 2 members being consecutive positive integers can be generated by^[17]

$x^{2} %2B (x%2B1)^{2} %2B \cdots %2B (x%2Bq)^{2} %2B p^{2} = (p%2B1)^{2}$

where q = n − 3 ≥ 0, where

$p = \frac{(q%2B1)x^{2} %2B q(q%2B1)x %2B q(q%2B1)(2q%2B1)/6 -1}{2},$

and where x must be chosen with parity (even or odd) such that p is an integer.

And Pythagorean n-tuples with the first k=n–1 members being consecutive positive integers can be generated by ^[18]

$a^2 %2B ... %2B (a%2Bk-1)^2 = b^2$

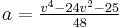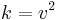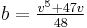where $a=\tfrac{v^4-24v^2-25}{48}$ , $k=v^2$ , $b=\tfrac{v^5%2B47v}{48}$ , and v is any integer not divisible by 2 or 3.

Fermat's Last Theorem

Main article: Fermat's Last Theorem

A generalization of the concept of Pythagorean triples is the search for triples of positive integers a, b, and c, such that aⁿ + bⁿ = cⁿ, for some n strictly greater than 2. Pierre de Fermat in 1637 claimed that no such triple exists, a claim that came to be known as Fermat's Last Theorem because it took longer than any other conjecture by Fermat to be proven or disproven. The first proof was given by Andrew Wiles in 1994.

n − 1 or n n^th powers summing to an n^th power

Main article: Euler's sum of powers conjecture

Another generalization is searching for sets of n + 1 positive integers for which the n^th power of the last is the sum of the n^th powers of the previous terms. The smallest sets for known values of n are:

n = 3: {3, 4, 5; 6}.
n = 4: {30, 120, 272, 315; 353}
n = 5: {19, 43, 46, 47, 67; 72}
n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}

A slightly different generalization allows the sum of (k + 1) nth powers to equal the sum of (n − k) nth powers. For example:

(n = 3): 1³ + 12³ = 9³ + 10³, made famous by Hardy's recollection of a conversation with Ramanujan about the number 1729 being the smallest number that can be expressed as a sum of two cubes in two distinct ways.

There can also exist n − 1 positive integers whose n^th powers sum to an n^th power (though, by Fermat's last theorem, not for n = 3); these are counterexamples to Euler's sum of powers conjecture. The smallest known counterexamples are

n = 4: (95800, 217519, 414560; 422481)
n = 5: (27, 84, 110, 133; 144)

Heronian triangle triples

Main article: Heronian triangle

A Heronian triangle is commonly defined as one with integer sides whose area is also an integer, and we shall consider Heronian triangles with distinct integer sides. The lengths of the sides of such a triangle form a Heronian triple (a, b, c) provided a < b < c. Clearly, any Pythagorean triple is a Heronian triple, since in a Pythagorean triple at least one of the legs a, b must be even, so that the area ab/2 is an integer. Not every Heronian triple is a Pythagorean triple, however, as the example (4, 13, 15) with area 24 shows.

If (a, b, c) is a Heronian triple, so is (ma, mb, mc) where m is any positive integer greater than one. The Heronian triple (a, b, c) is primitive provided a, b, c are pairwise relatively prime (as with a Pythagorean triple). Here are a few of the simplest primitive Heronian triples that are not Pythagorean triples:

(4, 13, 15) with area 24

(3, 25, 26) with area 36

(7, 15, 20) with area 42

(6, 25, 29) with area 60

(11, 13, 20) with area 66

(13, 14, 15) with area 84

(13, 20, 21) with area 126

By Heron's formula, the extra condition for a triple of positive integers (a, b, c) with a < b < c to be Heronian is that

(a² + b² + c²)² − 2(a⁴ + b⁴ + c⁴)

or equivalently

2(a²b² + a²c² + b²c²) − (a⁴ + b⁴ + c⁴)

be a nonzero perfect square divisible by 16.

Notes

^ "Euclid's Elements: Book X , Proposition XXIX". http://babbage.clarku.edu/~djoyce/java/elements/bookX/propX29.html.
^ Mitchell, Douglas W., "An alternative characterisation of all primitive Pythagorean triples," Mathematical Gazette July 2001,.
^ Rosenberg, Steven; Spillane, Michael; and Wulf, Daniel B., "Heron triangles and moduli spaces", Mathematics Teacher 101, May 2008, 656—663.
^ Beauregard, Raymond A., and Suryanarayan, E. R., "Parametric representation of primitive Pythagorean triples", in Nelsen, Roger B., Proofs Without Words II, Mathematical Association of America, 2000: p. 120.
^ Maor, Eli, The Pythagorean Theorem, Princeton University Press, 2007: Appendix B.
^ Sierpinski, Waclaw. Pythagorean Triangles, Dover, 2003: pp. 4–7.
^ Houston, David, "Pythagorean triples via double-angle formulas", in Nelsen, Roger B., Proofs Without Words , Mathematical Association of America, 1993: p. 141.
^ ^a ^b ^c Carmichael, R. D., 1914, "Diophantine analysis," in second half of R. D. Carmichael, The Theory of Numbers and Diophantine Analysis, Dover Publ., 1959.
^ ^a ^b ^c Sierpinski, Wacław (2003), Pythagorean Triangles, Dover Publications, ISBN 0-486-43278-5 , pp.23-25.
^ Bernhart, Frank R. and Price, H. Lee (2005). "Heron's formula, Descartes circles, and Pythagorean triangles". arXiv:math/0701624v1.
^ "Multiplying Pythagorean Triples". http://www.pythag.net/node9.html.
^ *Stillwell J (2003), Elements of Number Theory, New York: Springer-Verlag, pp. 110–112, ISBN 0-387-95587-9, http://books.google.com/books?id=LiAlZO2ntKAC&pg=PA110 .
^ Gauss CF (1832), "Theoria residuorum biquadraticorum", Comm. Soc. Reg. Sci. Gött. Rec. 4. See also Werke, 2:67–148.
^ 1988 Preprint See Figure 2 on page 3., later published as Multiple Pythagorean number triples Albert Fässler, American Mathematical Monthly, v.98 n.6, pages 505-517, June/July 1991 ( 10.2307/2324870)
^ Pythagorean triangles with legs less than n by Manuel Benito and Juan L. Varona, Journal of Computational and Applied Mathematics 143 (2002) 117–126
^ "A Collection of Algebraic Identities: Sums of n Squares". http://sites.google.com/site/tpiezas/005b.
^ Goehl, John F. Jr., "Reader reflections," Mathematics Teacher 98(9), May 2005, 580.
^ Hirschhorn, Michael, "When is the sum of consecutive squares a square?", Mathematical Gazette 95, November 2011, 511−512.

References

Alperin, Roger C. (2005), "The modular tree of Pythagoras", American Mathematical Monthly (Mathematical Association of America) 112 (9): 807–816, doi:10.2307/30037602, JSTOR 30037602, MR 2179860, http://www.math.sjsu.edu/~alperin/pt.pdf
Berggren, B. (1934), "Pytagoreiska trianglar" (in Swedish), Tidskrift för elementär matematik, fysik och kemi 17: 129–139
Barning, F.J.M. (1963), "Over pythagorese en bijna-pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices" (in Dutch), Math. Centrum Amsterdam Afd. Zuivere Wisk. ZW-011: 37, http://oai.cwi.nl/oai/asset/7151/7151A.pdf
Eckert, Ernest (1992), "Primitive Pythagorean triples", The College Mathematics Journal (Mathematical Association of America) 23 (5): 413–417, doi:10.2307/2686417, JSTOR 2686417
Elkies, Noam, Pythagorean triples and Hilbert's theorem 90, http://www.math.harvard.edu/~elkies/Misc/hilbert.pdf .
Heath, Thomas (1956), The Thirteen Books of Euclid's Elements Vol. 1 (Books I and II) (2nd ed.), Dover Publications, ISBN 0-486-60088-2 .
Martin, Artemas (1875), "Rational right angled triangles nearly isosceles", The Analyst (Annals of Mathematics) 3 (2): 47–50, doi:10.2307/2635906, JSTOR 2635906
McCullough, Darryl (2005), "Height and excess of Pythagorean triples", Mathematics Magazine 78 (1), http://www.math.ou.edu/~dmccullough/teaching/pythagoras2.pdf
Romik, Dan (2004), "The dynamics of Pythagorean triples", Eprint arXiv:math/0406512: 6512, arXiv:math.DS/0406512, Bibcode 2004math......6512R
Teigen, M. G.; Hadwin, D. W. (1971), "On Generating Pythagorean Triples", The American Mathematical Monthly (Mathematical Association of America) 78 (4): 378–379, doi:10.2307/2316903, JSTOR 2316903
Trautman, Andrzej (1998), "Pythagorean spinors and Penrose twistors", in S.A. Hugget, L.J. Mason, K.P. Tod, S.T. Tsou, N.M.J. Woodhouse, Geometric universe, http://www.fuw.edu.pl/~amt/oxford.ps .

External links

Weisstein, Eric W., "Pythagorean Triple" from MathWorld.
Pythagorean Triples at cut-the-knot Interactive Applet showing unit circle relationships to Pythagorean Triples
The Trinary Tree(s) underlying Primitive Pythagorean Triples at cut-the-knot
Theoretical properties of the Pythagorean Triples and connections to geometry
Clifford Algebras and Euclid's Parameterization of Pythagorean triples
Pythagorean Triplets
Discussion of Properties of Pythagorean triples, Interactive Calculators, Puzzles and Problems
Generating Pythagorean Triples Using Arithmetic Progressions
Parameterization of Pythagorean Triples by a single triple of polynomials
Curious Consequences of a Miscopied Quadratic
Solutions to Quadratic Compatible Pairs in relation to Pythagorean Triples
The negative Pell equation and Pythagorean triples
The Remarkable Incircle of a Triangle
Interactive Calculator for Pythagorean Triples
Price, H. Lee (2008), "The Pythagorean Tree: A New Species", Eprint arXiv:0809.4324 0809: 4324, arXiv:0809.4324, Bibcode 2008arXiv0809.4324P
Pythagorean Triples and the Unit Circle, chap. 2-3, in "A Friendly Introduction to Number Theory" by Joseph H. Silverman, 3rd ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ, ISBN 0-13-186137-9